[最も共有された！ √] z 変換 公式 281841

06/03/21 · オイラーの公式 指数法則と加法定理 他にもいろいろ嬉しいことがある 複素数の指数関数 高校数学では三角関数や指数関数を習いますが，その定義域は実数です。 実は，一般に複素数 z z z の三角関数 sin ⁡ z, cos ⁡ z \sin z,\cos z sin z, cos z や指数関数 e z e^z e z を考えることもできます1 r 2 µ @z @µ ¶2 = £ ¡fx sinµ fy cosµ ⁄2 となり、これから求める式が得られる。 14 (2) Chain Rule（連鎖公式）に慶應義塾 理工学部 物理情報工学科 物理情報数学C講師 足立修一教科書 足立修一：信号・システム理論の基礎～フーリエ解析・ラプラス変換・z

Z変換 ｓ領域から離散領域に変換 によるプログラム 技術メモ

Z 変換 公式

Z 変換 公式-「岩波数学公式集Ⅲ」p48では誤った式が書かれているので注意せよ。 楕円関数の虚数変換 ヤコビの楕円関数はテータ関数の比により表される。楕円関数の周期を, ′ とすると = ′3． z変換の定義 ここでは、z変換について簡単に解説します。 z変換の定義を示します。 サンプル値列 ｛x n ｝ ( n=0,1,2,‥) が与えられたとき、 を ｛x n ｝ の z変換 といいます。 z変換とラプラス変換は密接な関係があります。

スペクトル解析 第６回

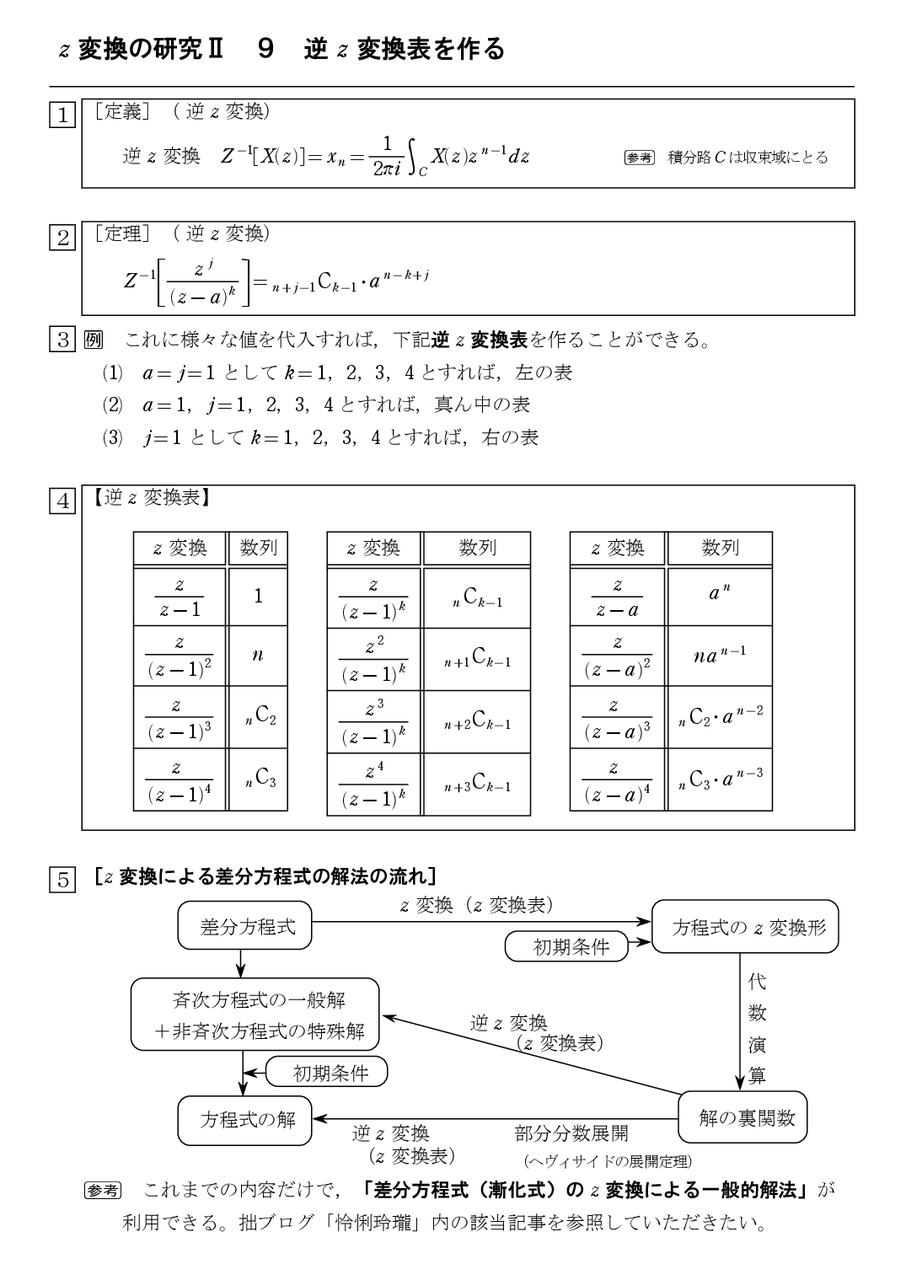
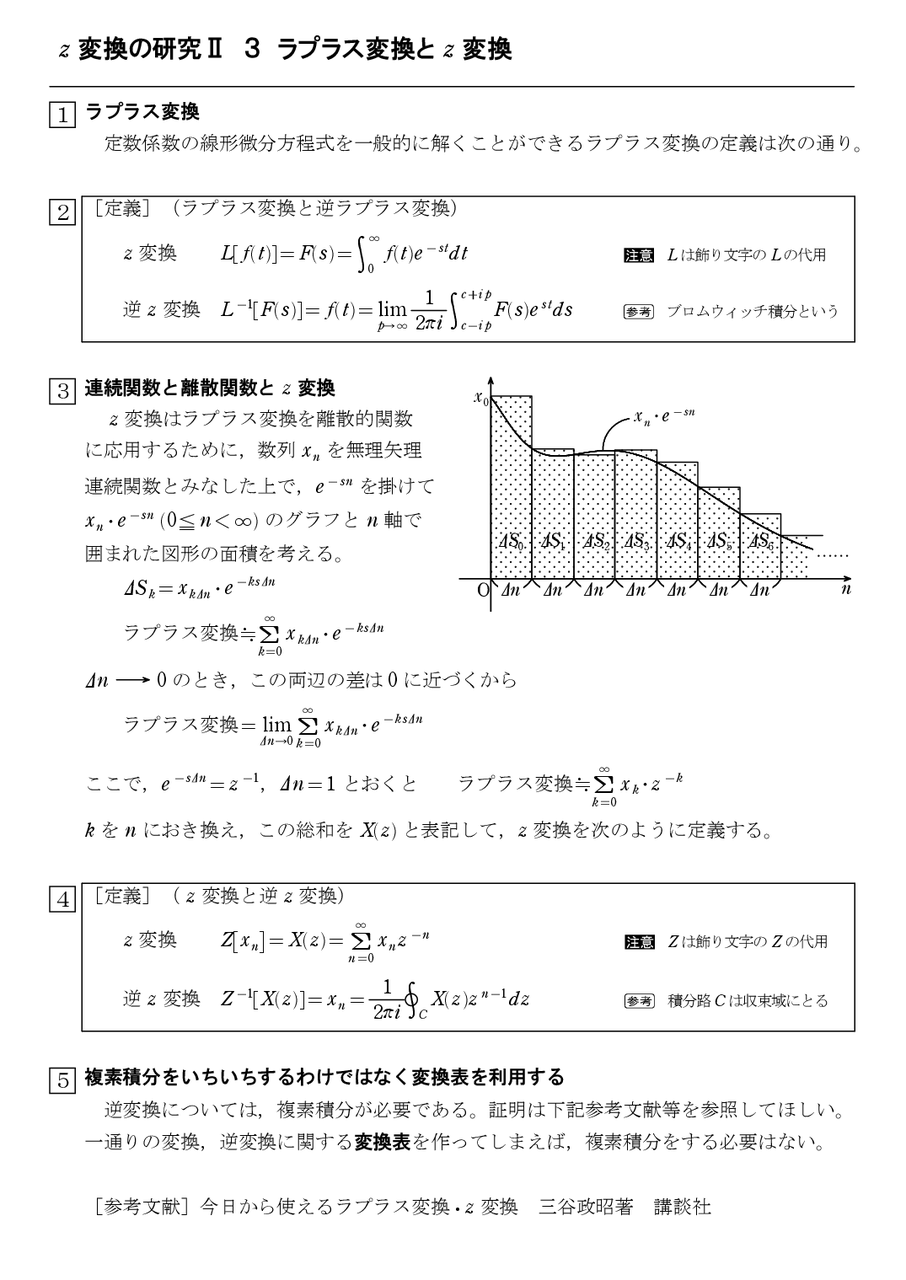
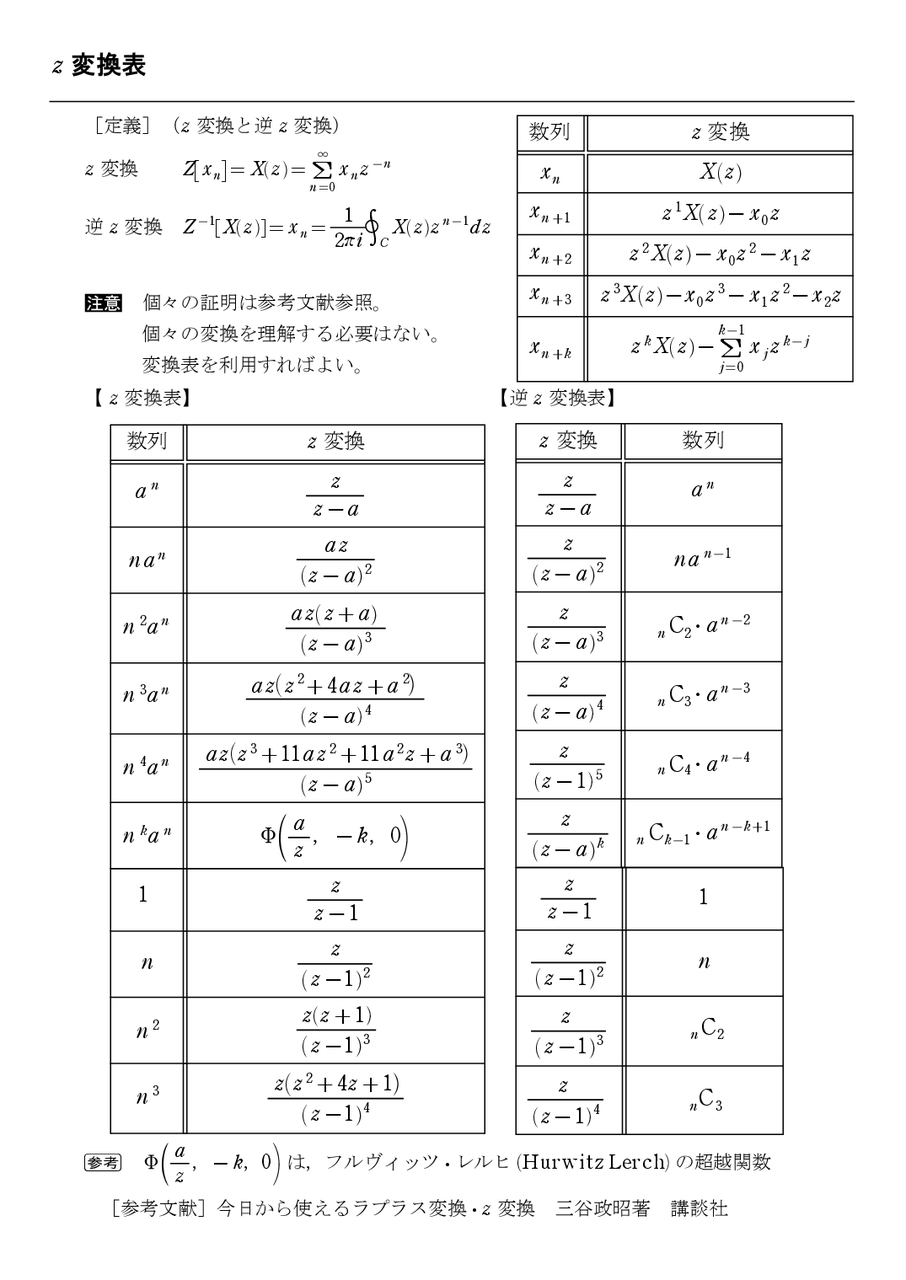
Ztrans(f1 f2,x,a b) ans = a/(a exp(1)), b/(b 1)^2 Z 変換が求まらない場合 ztrans が入力を変換できない場合は、第6週 逆 z 変換と伝達関数 教科書 p85 ～「逆 z 変換」 目標目目標標目標 ：逆z変換の方法と応用を学ぶ。離散線形時不変システムの伝達関数の理解。 ①逆z変換の演習 ②伝達関数 ③伝達関数と周波数応答 逆 z 変換とは z領域の表現から時間領域の信号を求めること 逆 z 変換定理 1 1 ( ) ( ) 2 n C x n定義(z 変換と逆z 変換) z 変換 Z =X(z)=∑ z 逆z 変換 Z X(z)= = 1 2πi X(z)z dz 注意 個々の証明は参考文献参照。 個々の変換を理解する必要はない。 変換表を利用すればよい。 数列 z 変換 X(z)

Z 変換表 表中の数字は、rとz'の対応を表します。 たとえば r =40場合はz'は「42」となります。〔〔〔〔5555〕〕〕〕有限長の信号の有限長の信号の有限長の信号のz zzz変換は簡単変換は簡単変換は簡単 −= − =⋯ − − ⋯ ⋯ ∞ =−∞ ∑ n k n X z( ) ( ) x n z x ( 2) z x ( 1) z x (0) z0 x (1) z1 x (2) z2 ( ) x k z 例： = = = = ⋯それ以外 ⋯ ⋯ ⋯ 0 1 2 2 1 3F(z) = ∞ ∑ n = 0fnz n F ( z) = ∞ ∑ n = 0 f n z − n (95) 例えば f 0 = 3, f 1 = 1, f 2 = 4, f n = 0, ( n > 2) となる数列 f n の Z 変換は以下の通りとなる． F(z) = ∞ ∑ n = 0fnz n = 3 z 1 4z 2 F ( z) = ∞ ∑ n = 0 f n z − n = 3 z − 1 4 z − 2 (96) ここで z は 複素数 で z = eTs = eT(σ jω) = re jωT と表す事が多い．

08/04/18 · というわけで、最後にもう1つ具体例を書いておきます。 全微分を利用して\(\sqrt{295^2 403^2}\) の近似値を求めよにより定義される複素関数 $\textrm{F}(z)$ をZ平面上の(片側)Z変換という。 また逆変換は以下の様に簡単に求まります。 定義 (片側) 逆 Z 変換Z変換の公式 (の一部) x(n)とy(n)のZ変換が各々X(z)とY(z)であるとき、 a x(n) b y(n) → a X(z) b X(z) x(nm) → zm X(z) が成立する。

重積分の変数変換とヤコビアン リーマン空間における多重積分

重積分の変数変換とヤコビアン リーマン空間における多重積分

また，f^ 2 L1(R) であれば，逆変換も成立する． 定理2 (フーリエ逆変換) L1 関数f 2 L1(R) に対してf^2 L1(R) ならば f(x) = ∫1 1 f^(˘)e2ˇi˘xdx (x 2 R) が成立する． 証明 2, p 44, 定理11 参照．正則関数と関係した特別な場合のフーリエ逆変換公式の 証明は後で行う(定理9)． 次に，フーリエ変換の基本的@y @r = sinµ;Z 変換の場合も， えー，そんな総和の公式初めて見たお． やらない夫 まあ，この計算ができること自体はそれほど重要じゃない．必要になったときに参考書の変換表を見れば済むことだ．それよりも，特性方程式が重解を持つ場合も，それに対応して出てくる応答は指数関数 に 高々 の多項

双一次変換とは 制御工学の基礎あれこれ

双一次変換とは 制御工学の基礎あれこれ

でも逆 z 変換の公式を使うのは面倒だお． やらない夫 なので，普通は何らかの式変形をした上で，z 変換表を見ながら置き換えていくのが常套手段だ．ラプラス変換のときと同じように，当面必要なものだけ抜粋しておこうか．Offliberty lets you access any online content without a permanent Internet connection Today most websites are difficult to browse offline If you have limited access to the Internet you can use Offliberty to browse any content later being offline22 基本的な変換 13 22 基本的な変換 αは複素定数で，a，θ0 は実定数とする。 （1）平行移動 ω= zα この変換により，z平面内の図形は，αだけ平行移動される。 （2）回転 ω=eiθ0 z= (cosθ0 isinθ0)z この変換により，z平面内の図形は，原点を中心にして角θ0 だけ回転される。

Z 変換 怜悧玲瓏 高校数学を天空から俯瞰する

14 Z 変換 やる夫で学ぶディジタル信号処理

定義 列 xn のZ変換は以下の式で定義される Z x n = X ( z ) = ∑ n = − ∞ ∞ x n z − n {\displaystyle {\mathcal {Z}} x_ {n}=X (z)=\sum _ {n=\infty }^ {\infty }x_ {n}z^ {n}} ここで n は 整数 で z は 複素数 である。 なお後述の片側Z変換に対してこれを 両側Z変換 （twosided Ztransform、bilateral Ztransform）と呼ばれる。 n06/03/21 · 底の変換公式の使い方のコツ 底の変換公式： log ⁡ a b = log ⁡ c b log ⁡ c a \log_a b=\dfrac{\log_c b}{\log_c a} lo g a b = lo g c a lo g c b は「対数の底を a a a から c c c に変換できる」と見ることができます。そのため，底の変換公式は，対数の底をそろえるために使わAmazonで博, 原島, 洋一, 堀の工学基礎 ラプラス変換とz変換 (新・工科系の数学)。アマゾンならポイント還元本が多数。博, 原島, 洋一, 堀作品ほか、お急ぎ便対象商品は当日お届けも可能。また工学基礎 ラプラス変換とz変換 (新・工科系の数学)もアマゾン配送商品なら通常配送無料。

底の変換公式をしてもlog10の3は消えませんでした計算の過程を教えて欲しいです Clear

Z変換をやさしく教えて下さい 音響学入門ペディア

21 z変換の基礎 31 図23 z変換の収束領域 214 数列と収束領域 〔1〕 有限数列 数列x(n)は有限値であるとする。 X(z)= n2 n=n1 x(n)z−n (212) 収束領域としては，n1 < 0のとき，zp,p>0 の項を含むのでz = ∞ を除き， n2 > 0のときはzp,p公式集 索引 数I 数A ホーム>>カテゴリー分類>>微分>>ラプラス変換>>三角関数のラプラス変換 学生スタッフ作成 初版：09年3月5日，最終更新日： 10年2月24日 ページトップ 利用規約 google translate (English version)Z変換を使うと まず入力xnをZ変換する。 信号は2入力なので、 である。 次にhnをZ変換する。 次に畳み込みのZ変換は、 つまり、 これを逆Z変換すると ゆえに このようにz変換を使うと畳み込みが単純な積となり簡単に計算できる。 これがz変換を使う第一の理由である。

14 Z 変換 やる夫で学ぶディジタル信号処理

ラプラス変換とz変換

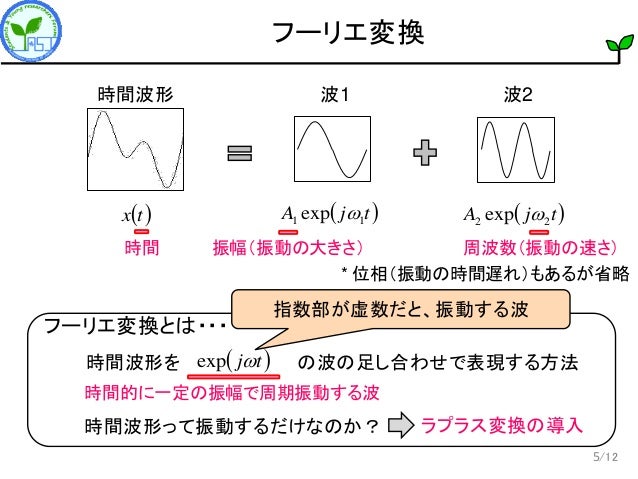
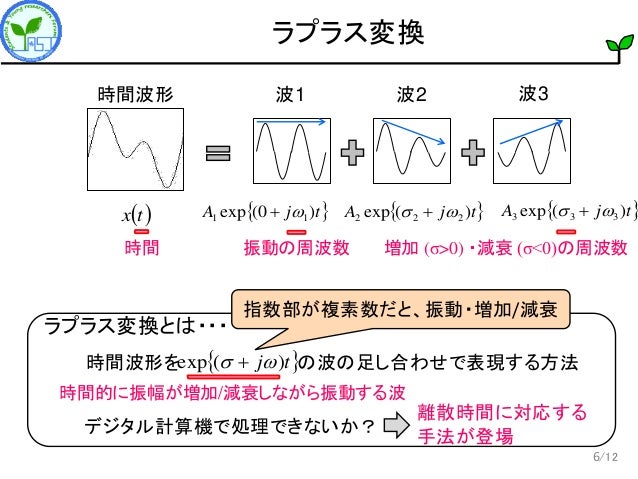
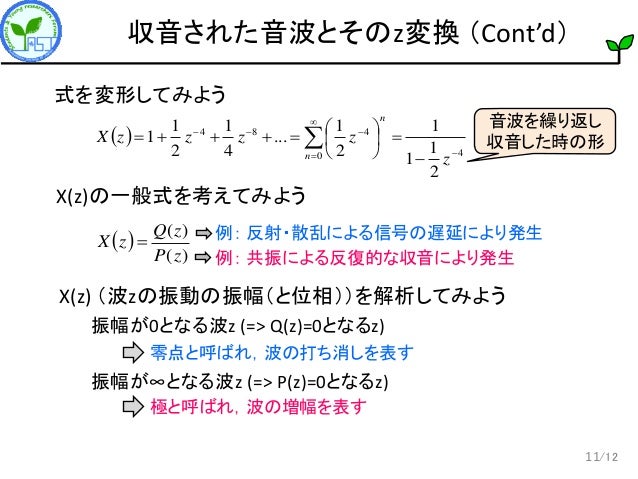
配列入力の逆 Z 変換 行列 M の逆 Z 変換を求めます。同じサイズの行列を使用して、各行列エントリの独立変数と変換変数を指定します。引数が非スカラーである場合、iztrans は各要素に適用されます。解 (1) Chain Rule (連鎖公式）により、 @z @r = @f @x @x @r @f @y @y @r;06/06/15 · z変換した結果と実際の音波ってどんな関係があるの？ z変換を学ぶ機会は少なからずあったはず 3 Z変換って何なの？ 3 4 /12 z変換の前に： 波の足し合わせによる表現 4 おてもやん 音源 音波 マイクロホン 収音された時間波形 時間波形を"何かの波"の足し合わせで表現することで， その

Z変換 ｓ領域から離散領域に変換 によるプログラム 技術メモ

Z 変換 怜悧玲瓏 高校数学を天空から俯瞰する

Z変換と呼ばれる変数変換を行う。 統計の分野でのz変換は、離散系の電子分野で使うz変換とは全く異なる。実にまぎらわしい。 統計ではこのz変換により、基準になるたった一つの正規分布として平均値がゼロ、 分散が1の標準化正規分布が得られる。ラプラス変換によって得られた連続型のs関数を、離散型のz関数に近似する双一次変換について説明します。s関数とz関数の関係は以下のとおり。 双一次変換とは 結果から示すと双一次変換式は以下となります。s関数に以下式を代入するとz関数に変換できます。後ほど具体例で示します。 何故質問・相談 逆z変換について x(z)=1/(z^215z05)の逆z変換を行います。 部分分数展開して x(z)=2{1/(z1)1/(z05)} ここから、どうすればよいのかわかりません。 留数定理による解法では、x(z)にz^(n1)を 数学 z/(z1)^2のラプラスの逆変換がわかりません泣 どなたか教えていた

双一次変換 Wikipedia

Mr Smithとインピーダンスマッチングの話 第10話 Sパラメータの基礎 19年8月号 月刊fbニュース アマチュア無線の情報を満載

12 Zパラメータ (opencircuit impedance parameters) V1 Z11 Z12 I1 = (12) V2 Z21 Z22 I2 ついては、以下に述べるSパラメータとZパラメータ、Yパラメータ、 hパラメータ等の変換公式を使って、 低周波で使われる標準的な手法を利用することもできます。差分方程式とz変換 差分方程式,漸 化式,z変 換,コ ンボリューション 浜田 望 1は じめに 離散時間システムを記述する基本式である差分方程式 (漸化式)にz変 換を利用した解析や実現がどのように有 効に利用されているかについて述べる。特に代数的な手法Z y x =0 この公式は，渦巻きの軸方向のベクトル自身は閉じていることを意味している．竜巻の 中心を流れる上昇気流を考えると良いが，気流が下から上に上がり，それが上で広がって やがて竜巻の外側を通って下方におりてくる．そしてまた吸いあがる．上昇気流を渦巻き の軸方向のベクトル

ヤコビの虚数変換式 Wikipedia

ラプラス変換とフーリエ変換 半導体事業 マクニカ

％Zは，インピーダンスZ〔Ω〕に基準電流（定格電流）I B 〔A〕が流れて， 生じた電圧降下と基準電圧（定格電圧）E B 〔kV〕との百分率である。 次の式は、1項のΩ→％Z変換式である。 この式から％ZをΩに変換する式を算出すると、43 ラプラス逆変換の計算公式（ヘヴィサイドの展開定理） 44 z 変換の意義と変換表の使い方 45 差分方程式の一般的な解法 46 逆z 変換の計算公式 47 線形システムと畳み込み処理 第5章 ラプラス変換によるアナログ・システム解析を理解しよう@x @µ = ¡rsinµ;

座標回転公式と球面三角法

ディジタルフィルタとｚ変換

ここで n は 整数 で z は 複素数 である。 なお後述の片側Z変換に対してこれを 両側Z変換 （twosided Ztransform、bilateral Ztransform）と呼ばれる。 n微分方程式変数変換による解き方 1階の常微分方程式について，何らかの変数変換を行うことによって解きやすい形に変えることは，この頁以前にも登場しています． 復習 (I) 同次形の微分方程式 =f() の形に書けるものは， z= とおけば z が x に関して変数分離形になります． →この頁参照（ ）が変換後の座標系における比例係数{lm}で，ちゃんとテンソルの変換の約束に従っている： lm = i,j U li ij (U −1) jm= i,j U li U mj ij 12 かけ算公式 ある方向の単位ベクトル（長さ1のベクトル）をe，また，x，y，z 方向の単位ベクトルを，それぞれ e x，e y，e z

Ehiコントロールシステムズのブログ

極座標と直交座標の変換公式 ２次元と３次元 Irohabook

34 Z 変換 341 Z変換の定義 離散信号 のZ変換は次式により定義されている。 C n X z z dz i x n ( ) 1 2 1 ( ) x n ( ) Z x n X z ( ) ( ) ただし、zは複素要素をとる複素変数である。また逆変換は と定義される。ただし、積分路Cは収束領域内での原点を内部@z @µ = @f @x @x @µ @f @y @y @µ また、 @x @r = cosµ;シンボリック関数の Z 変換を計算します。1 番目の引数がシンボリック関数を含む場合、2 番目の引数はスカラーでなければなりません。 syms f1(x) f2(x) a b f1(x) = exp(x);

Z 変換 怜悧玲瓏 高校数学を天空から俯瞰する

勉強しよう数学 ベクトルによる座標軸の回転変換の公式

@y @µ = rcosµ なので、 µ @z @r ¶2 = £ fx cosµ fy sinµ ⁄2;

Z変換 ｓ領域から離散領域に変換 によるプログラム 技術メモ

高校数学 変数変換による平均値 分散 標準偏差 共分散 相関係数の変化 受験の月

Z変換 ｓ領域から離散領域に変換 によるプログラム 技術メモ

4 1 変換行列とは

インピーダンス アドミタンスの変換式はこう解く 忘れた数学 興味を感じたexperimentを自由気ままに実践している備忘日記

Z変換をやさしく教えて下さい 音響学入門ペディア

ラプラス変換の復習 教科書には相当する章はない Ppt Download

宮崎技術研究所 自動制御講座 4 1 3 Z変換とパルス伝達関数 1 2

ディジタル信号処理 Digital Signal Processing Ppt Download

宮崎技術研究所 自動制御講座 4 1 3 Z変換とパルス伝達関数 1 2

Z変換をやさしく教えて下さい 音響学入門ペディア

双一次変換とは 制御工学の基礎あれこれ

Ppt デジタル信号処理 Powerpoint Presentation Free Download Id

漸化式 Wikipedia

ディジタル制御の基礎

高校数学 複素数平面上の反転変換w 1 Zによる像 受験の月

ラプラス変換の計算方法 理系大学院生の知識の森

Z変換をやさしく教えて下さい 音響学入門ペディア

特殊ローレンツ変換から一般ローレンツ変換へ

Z 変換 怜悧玲瓏 高校数学を天空から俯瞰する

ディジタル制御の基礎

Z変換をやさしく教えて下さい 音響学入門ペディア

Z 変換 怜悧玲瓏 高校数学を天空から俯瞰する

ラプラス変換とフーリエ変換 半導体事業 マクニカ

複素数の極形式表示

Z変換をやさしく教えて下さい 音響学入門ペディア

底の変換公式をしてもlog10の3は消えませんでした計算の過程を教えて欲しいです Clear

重積分の変数変換とヤコビアン リーマン空間における多重積分

高校数学 対称式の連立方程式 対称性を崩さずに求めよ 受験の月

14 Z 変換 やる夫で学ぶディジタル信号処理

母相関の検定と推定

Z変換をやさしく教えて下さい 音響学入門ペディア

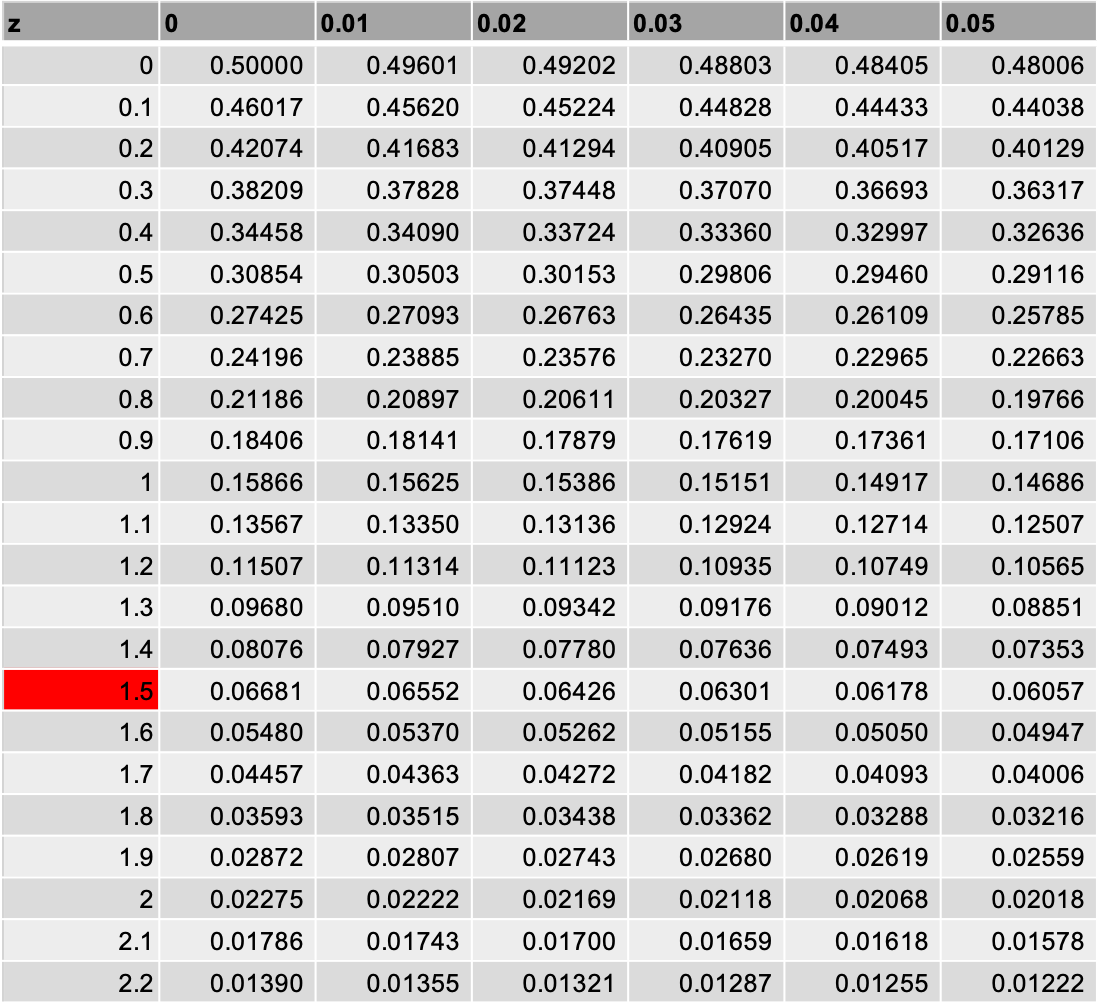
標準正規分布表の見方や使い方 標準化やz値の計算式はどうすればいい いちばんやさしい 医療統計

信号 システム理論の基礎 フーリエ解析 ラプラス変換 Z変換を系統的に学ぶ コロナ社

Z 変換 怜悧玲瓏 高校数学を天空から俯瞰する

14 Z 変換 やる夫で学ぶディジタル信号処理

Z変換チートシート Qiita

ディジタル信号処理 Digital Signal Processing Ppt Download

Z 変換の研究 ２ 研究結果の定理を鑑賞する 怜悧玲瓏 高校数学を天空から俯瞰する

ディジタルフィルタとｚ変換

双一次変換とは 制御工学の基礎あれこれ

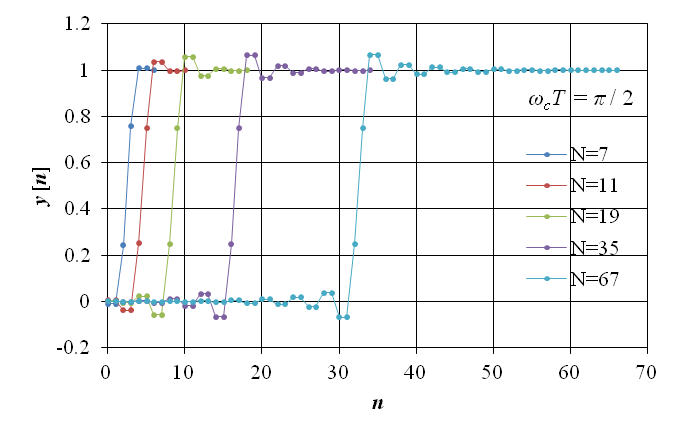
13 Fir フィルタの概要 趣味人のブログ

Z 変換の研究 ５ Z 変換表を作る 怜悧玲瓏 高校数学を天空から俯瞰する

9 ディジタル信号処理と Z 変換 趣味人のブログ

9 ディジタル信号処理と Z 変換 趣味人のブログ

Z変換 ｓ領域から離散領域に変換 によるプログラム 技術メモ

Z変換 Wikipedia

Z 変換 怜悧玲瓏 高校数学を天空から俯瞰する

ラプラス変換とその使い方１ 基礎編 ラプラス変換とは何か 変換の基礎事項は 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会

Z変換をやさしく教えて下さい 音響学入門ペディア

Z変換をやさしく教えて下さい 音響学入門ペディア

14 Z 変換 やる夫で学ぶディジタル信号処理

Z 変換の研究 ２０ 自然数の R 乗和の公式 怜悧玲瓏 高校数学を天空から俯瞰する

スマホで学ぶ 実践ディジタル信号処理入門

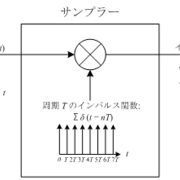
9 ディジタル信号処理と Z 変換 趣味人のブログ

双一次変換とは 制御工学の基礎あれこれ

梅崎直也 画像間違ってたので再ツイート 僕も漸化式 の話は線形代数の好きなところの一つですね そのあたりの微分方程式と数列の話の類似でラプラス変換とか関数解析とかに関わる話は前に一度数学カフェの予習会でお話しさせてもらいました T Co

Z 変換 怜悧玲瓏 高校数学を天空から俯瞰する

Fパラメータ Sパラメータ変換 第五回 全五回 ゆうテックぶろぐ

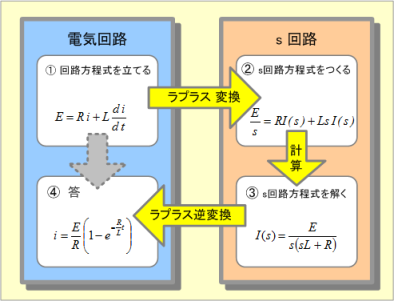
ラプラス変換とその使い方１ 基礎編 ラプラス変換とは何か 変換の基礎事項は 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会

Z変換 Z Transform Japaneseclass Jp

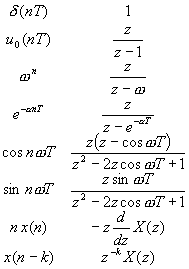
ディジタルフィルタを作ってみよう

ラプラス変換とフーリエ変換 半導体事業 マクニカ

三角関数の公式

スペクトル解析 第６回

Fパラメータ Sパラメータ変換 第五回 全五回 ゆうテックぶろぐ

ラプラス変換 Wikipedia